Start the conversation
There's one eensy number that every pro trader checks out when they're doing their "homework" before picking a trade.
They clean up on those trades, and now, so will you...
You see, we know that the options on the stocks that have a $0.05 or less bid/ask spread, like you find on the CBOE Penny Pilot list, give you the best chance at making the most money on the smallest price moves.
And we know that picking an option with the lowest "percent to double" gives you an easy shot at doubling your money when you want that to happen.
But now I want to show you how to use one number to pick the options that will move in your favor when the stock you're trading moves in price before you enter the trade.
This number is always between -1.00 and 1.00. Oddly enough, plenty of casual traders never consider using it, so they miss out on some big profits. Maybe that's because it has a funny-sounding Greek name...
This Algebra Is Scary (but You'll Never Have to Use It)
There's a rather complicated equation to solve to figure out how much your option will move in relation to the underlying share price.
It goes like this...
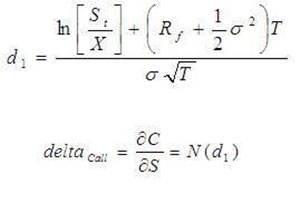
Looks horrible, right?
Well, the good news is you don't have to worry about it (unless you really like algebra), because your brokerage and even a few free websites - like the Chicago Board Options Exchange (CBOE) - will solve that equation for you and present you with a nice, neat, small, manageable number - a number we call "delta" (δ)
Delta (δ) is one of the options "Greeks" that determine an option's risk, and therefore its premium or value. It is considered by many, including myself, to be the most important component of an option.
Delta (δ) can be used in a couple of different ways when you're trading options. I'll show you the single most useful way to use it - and why it's really helpful in determining just which option to buy.
Here's Everything Delta (δ) Can Tell You
In simple terms, delta (δ) is a numerical value given to each option that shows how much that option's premium will move with the next $1 move in the stock.
Delta is either a positive number (for calls) or a negative number (for puts). Call options will have a value of anywhere from 0 to 1.00, while put options have a value anywhere from -1.00 up to 0.
Now, every once in a while, you'll see delta (δ) expressed as a percentage, in which case it will range from -100.00% to 100.00%, but that's no biggie. It means the same thing.
Here's a quick example: take a stock trading at $50 with a call option that has a delta of .60.
That means when the stock goes $1.00 higher, that call option should go up $0.60 in price on the delta component alone. On one contract, that means an increase of $60, since one contract grants control of 100 shares.
With a put, take that same stock at $50. If you look at a put option that has a -0.60 delta, that means when the stock drops in price by $1.00, the put option price, on the delta component alone, should go up $0.60, or $60 per contract.
Mind you, the delta will work against you by that same amount should the stock move against you. For example, if you have a call option with a 0.60 delta and the stock drops $1.00, that call option should drop that 0.60, or $60 on the contract.
The delta value of an option plays an outsized role in determining that option's profitability. An option's "moneyness" (that is, whether it's in the money, at the money, or out of the money) directly impacts the delta value.
More specifically, the delta tells you the probability of the option ending up in the money at expiration.
About the Author
Tom Gentile, options trading specialist for Money Map Press, is widely known as America's No. 1 Pattern Trader thanks to his nearly 30 years of experience spotting lucrative patterns in options trading. Tom has taught over 300,000 traders his option trading secrets in a variety of settings, including seminars and workshops. He's also a bestselling author of eight books and training courses.
