Last week, I gave you an in-depth look at delta, a major component of options pricing that can tell you how much your option will move in relation to moves in the stock price.
But there are a few more "Greeks" you'll need to know if you want to be successful at options trading.
If you've been with me for a while, then you know that volatility has a huge impact on options pricing, but we haven't really covered the mechanics of how that happens, or what it means for your money.
Understanding today's lesson is crucial - I'm going to show you how to find stocks with a chance to make big moves... and how to identify potentially lucrative options plays to profit on those moves.
We're going to explore in detail the Greek that measures changes of an option's value based on how much the implied volatility (IV) on the underlying security changes.
Let's take a look...
Real Value vs. Time Value
 An option premium has two primary components to it: intrinsic value and extrinsic (time) value.
An option premium has two primary components to it: intrinsic value and extrinsic (time) value.
Intrinsic value, also called real value, is the amount an option is in the money (ITM).
For example, if a stock is trading at $47, then a $45 call option would be ITM by $2.00.
The reason it is deemed ITM is because the strike price is less than the stock price, which means the call option has real value of $2 because the call option allows the buyer the right to buy the stock at $45 while it's selling on the open market for $47. That's a built-in profit, or intrinsic value, which is governed by delta.
Now, technically there may not be an actual realized profit because the option would cost a bit more than $2 thanks to the extrinsic value component.
Extrinsic value is the amount of the premium that is paying for the time value of the option. If an option is ITM, it has both intrinsic value and extrinsic value until expiration. Out of the money (OTM) options, however, have no intrinsic value - 100% of an OTM option's value is extrinsic.
The extrinsic value of an option is determined by the implied volatility (IV) of the underlying, which is measured by the options Greek known as vega.
Vega is a calculated value showing the theoretical change in price for an option for every 1% change in volatility in the underlying asset.
Take for example an option that is trading at $3.00 with a vega of 0.15, or 15%. When the IV goes from 24% to 25%, the option, on vega alone, should theoretically increase to $3.15.
Measuring Volatility
When IV rises, the option price rises along with it and vice versa.
IV has an effect on the price of options as it estimates the potential magnitude of a move in a security in either direction. It's what the markets believe an underlying asset's historical volatility will be going forward based on changes in the options price.
An asset with a high IV will make a larger move than an asset with low IV and is more likely make a move in your favor if you're trading options. A low IV indicates the asset is expected to stay pretty flat or not move that much at all, which means your options would have less of a chance to move.
The higher the IV, the higher the extrinsic value of the options will be. Since extrinsic value is priced into an option's premium, whether they be ITM or OTM, the higher the extrinsic value, the more expensive these options will be.
As IV increases, the price of the options increase, making them more and more expensive. If you own options and the IV increases, your options should increase in value.
This whole scenario is represented in all options contracts by vega.
IV usually increases with expectations. For example, an anticipated news event could cause a stock to make a dramatic move because that event draws in more and more traders to it (and its options).
The most common scenario is a company's earnings report. Here is the domino effect: The company has an upcoming earnings report. More and more traders start speculating that the company will beat estimates and start buying call options at an accelerated pace.
The market makers can increase the price of the options due to this increased demand. IV can be plotted as you see below:
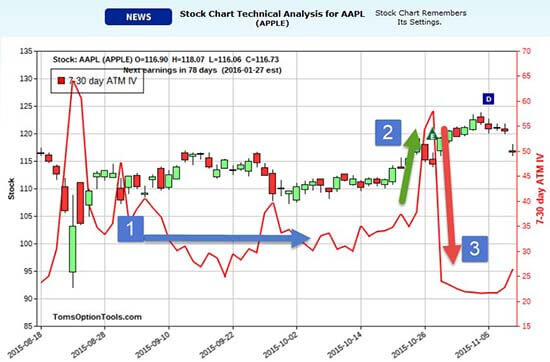
What you see is the 7-30 day implied volatility for Apple Inc. (Nasdaq: AAPL). Here's how it breaks down:
- Prior to its earnings date, IV was fairly flat, or at least maintained in a range.
- Notice the ramp-up in IV going into the day of APPL's earnings.
- Post-earnings, IV drops off precipitously.
Don't Get Crushed
IV can ramp up and carry an option's value via the option's vega, but it can also wipe a huge portion of the option's value once the IV drops, as it typically does after an earnings announcement.
This is what I call a volatility crush!
[mmpazkzone name="in-story" network="9794" site="307044" id="137008" type="4"]
When IV drops, so do options with positive vega. This is what makes options trading at earnings a risky game, especially for those traders who want to risk holding the options over the earnings announcement. If you hold your options over earnings, make sure you have some good analysis tools at your disposal.
Here's the ideal situation: Buy low IV options in advance of a news event like earnings. Assess the vega and know what amount it can increase theoretically with each 1% move in IV on the stock. When the stock ramps up into the announcement, consider selling the option ahead of earnings and eliminate the risk of a volatility crush.
Now, on straight call or put buys, I favor ITM options, so vega isn't the most important thing I evaluate, but it still helps me assess the impact IV will have on an option's extrinsic value.
Follow us on Twitter @moneymorning or like us on Facebook.
Four Steps to Options Trading Success: Many investors stay away from options, finding them risky or overwhelming. But you don't have to be afraid. Understanding these four rules will help you calculate reward, manage risk, and trade options with confidence...
About the Author
Tom Gentile, options trading specialist for Money Map Press, is widely known as America's No. 1 Pattern Trader thanks to his nearly 30 years of experience spotting lucrative patterns in options trading. Tom has taught over 300,000 traders his option trading secrets in a variety of settings, including seminars and workshops. He's also a bestselling author of eight books and training courses.



